Na teoria da probabilidade e na estatística, a distribuição de Poisson é uma distribuição de probabilidade discreta que expressa a probabilidade de uma série de eventos ocorrer num certo período de tempo se estes eventos ocorrem independentemente de quando ocorreu o último evento.
A distribuição foi descoberta por Siméon-Denis Poisson(1781–1840) e publicada, conjuntamente com a sua teoria da probabilidade, em 1838 no seu trabalho Recherches sur la probabilité des jugements en matières criminelles et matière civile ("Inquérito sobre a probabilidade em julgamentos sobre matérias criminais e civis"). O trabalho focava-se em certas variáveis aleatórias N que contavam, entre outras coisas, o número de ocorrências discretas (por vezes chamadas de "chegadas") que tinham lugar durante um intervalo de tempo de determinado comprimento. A probabilidade de que existam exactamente k ocorrências (k sendo um inteiro não negativo, k = 0, 1, 2, ...) é
onde
- e é base do logaritmo natural (e = 2.71828...),
- k! é o fatorial de k,
- λ é um número real, igual ao número esperado de ocorrências que ocorrem num dado intervalo de tempo. Por exemplo, se o evento ocorre a uma média de 4 minutos, e estamos interessados no número de eventos que ocorrem num intervalo de 10 minutos, usariámos como modelo a distribuição de Poisson com λ = 10/4 = 2.5.
Como função de k, esta é a função de probabilidade. A distribuição de Poisson pode ser derivada como um caso limite da distribuição binomial.
Índice[esconder] |
[editar]Processo de Poisson
A distribuição de Poisson aparece em vários problemas físicos, com a seguinte formulação: considerando uma data inicial (t = 0), seja N(t) o número de eventos que ocorrem até uma certa data t. Por exemplo, N(t) pode ser um modelo para o número de impactos de asteróides maiores que um certo tamanho desde uma certa data de referência.
Uma aproximação que pode ser considerada é que a probabilidade de acontecer um evento em qualquer intervalo não depende (no sentido de independência estatística) da probabilidade de acontecer em qualquer outro intervalo disjunto.
Neste caso, a solução para o problema é o processo estocástico chamado de Processo de Poisson, para o qual vale:
em que λ é uma constante (de unidade inversa da unidade do tempo).
Ou seja, o número de eventos até uma época qualquer t é uma distribuição de Poisson com parâmetro λ t.
[editar]Propriedades
[editar]Média
O valor esperado de uma distribuição de Poisson é igual a λ. Esta propriedade pode ser derivada facilmente[1]:
| Em linguagem matemática | Em Português |
|---|---|
![E \left [ X \right ] = \sum_{k=0}^{\infty} k\mathbb{P} \left [ X=k \right ]](http://upload.wikimedia.org/math/c/2/7/c27ac0030882c01f4e3ba068db722b84.png) | Por definição, a esperança de uma variável aleatória X é igual à soma de cada uma das suas possíveis ocorrências ponderadas pela probabilidade de que estas ocorrências aconteçam. |
![E \left [ X \right ] = \sum_{k=0}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!},\,\! \right ]](http://upload.wikimedia.org/math/a/e/b/aebe703a746ffbe5d9b0aa1375ab2ef8.png) | No caso de variáveis com distribuição, a probabilidade de que determinado evento ocorre é calculado por : . Portanto, este valor foi substituído na fórmula. . Portanto, este valor foi substituído na fórmula. |
![E \left [ X \right ] = \begin{matrix} \underbrace{ 0 \left [ \frac{e^{-\lambda} \lambda^0}{0!},\,\! \right ] } \\ k=0 \end{matrix} + \begin{matrix} \underbrace{ 1 \left [ \frac{e^{-\lambda} \lambda^1}{1!},\,\! \right ] } \\ k=1 \end{matrix} + \begin{matrix} \underbrace{ 2 \left [ \frac{e^{-\lambda} \lambda^2}{2!},\,\! \right ] } \\ k=2 \end{matrix}+...](http://upload.wikimedia.org/math/a/d/b/adb0a0229ccc29b8058a3c940151ccf9.png) | Esta expressão equivale à expressão da linha imediatamente superior; apenas se substituiu a expressão de somatório pela soma infinita para melhor compreensão. Note que como o primeiro termo é sempre igual a zero, podemos reescrever ![E \left [ X \right ] = \sum_{k=0}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ] = \sum_{k=1}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ]](http://upload.wikimedia.org/math/6/5/2/6526245ac47e35aab08be5c931a206b9.png) |
Como ![\sum_{k=1}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ]=\sum_{k=1}^{\infty} \lambda \left [ \frac{e^{-\lambda} \lambda^{k-1}}{(k-1)!} \right ]](http://upload.wikimedia.org/math/7/a/8/7a8c7133c2ec82362fa9aa9c077e1c1e.png) | Fazemos uma substituição para facilitar o cálculo. |
![E \left [ X \right ] =\lambda \sum_{k=1}^{\infty} \left [ \frac{e^{-\lambda}\lambda^{k-1}}{(k-1)!} \right ]](http://upload.wikimedia.org/math/6/2/b/62b46c1939d2c2ea1dedac233921c625.png) | Tomamos a substituição acima e tiramos a constante  para fora do somatório (pois o primeiro termo da expressão imediatamente superior é igual à para fora do somatório (pois o primeiro termo da expressão imediatamente superior é igual à  . . |
![E \left [ X \right ] = \lambda e^{-\lambda} \sum_{k=0}^{\infty} \left [ \frac{\lambda^{k}}{(k)!} \right ]](http://upload.wikimedia.org/math/b/e/6/be60a9e58ce6cc3ae36bbdf2e866896d.png) | Nova transformação para facilitar os cálculos... |
![E \left [ X \right ] = \lambda e^{-\lambda}](http://upload.wikimedia.org/math/2/6/d/26d1a16606b089bdf4cda7ebd2193d9b.png) ![\left [ \frac{\lambda^{0}}{(0)!}+ \frac{\lambda^{1}}{(1)!}+ \frac{\lambda^{2}}{(2)!}+\frac{\lambda^{3}}{(3)!}+... \right ]](http://upload.wikimedia.org/math/a/f/7/af767888596668554224b683dd2de9ba.png) | Abrindo o somatório, verifica-se que a série converge para  |
![E \left [X \right] = \lambda e^{-\lambda}e^{\lambda}](http://upload.wikimedia.org/math/8/b/7/8b75ff3b01bac2b16b47bf95e664c8fa.png) | Obtemos  |
![E \left [ X \right ] = \lambda](http://upload.wikimedia.org/math/e/1/7/e1757adeca54855d6ff40534c4d6d6aa.png) | Como queríamos demonstrar |
[editar]Variância
A variância de uma distribuição de Poisson é igual a λ.
[editar]Soma de variáveis
A soma de duas variáveis de Poisson independentes é ainda uma variável de Poisson com parâmetro igual à soma dos respectivos parâmetros. Ou seja, se  segue uma distribuição de Poisson com parâmetro
segue uma distribuição de Poisson com parâmetro  e as variáveis aleatórias
e as variáveis aleatórias  são estatisticamente independentes, então
são estatisticamente independentes, então
 segue uma distribuição de Poisson com parâmetro
segue uma distribuição de Poisson com parâmetro  e as variáveis aleatórias
e as variáveis aleatórias  são estatisticamente independentes, então
são estatisticamente independentes, então-
 também segue uma distribuição de Poisson cujo parâmetro é igual à soma dos
também segue uma distribuição de Poisson cujo parâmetro é igual à soma dos  .
.
Por exemplo, 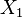 é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e  é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média 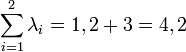 .
.
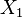 é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e  é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média 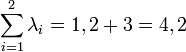 .
.[editar]Intervalo de confiança
Um método rápido e fácil para calcular um intervalo de confiança de aproximada de λ, é proposto na Guerriero (2012)[2]. Dado um conjunto de eventos k (pelo menos 15 - 20) ao longo de um período de tempo T, os limites do intervalo confiança para a frequência são dadas por:
em seguida, os limites do parâmetro  são dadas por:
são dadas por:  .
.
 são dadas por:
são dadas por:  .
.[editar]Exemplos
A distribuição de Poisson representa um modelo probabilístico adequado para o estudo de um grande número de fenômenos observáveis. Eis alguns exemplos:
- Chamadas telefônicas por unidade de tempo;
- Defeitos por unidade de área;
- Acidentes por unidade de tempo;
- Chegada de clientes a um supermercado por unidade de tempo;
- Número de glóbulos sangüíneos visíveis ao microscópio por unidade de área;
- Número de partículas emitidas por uma fonte de material radioativo por unidade de
tempo.
[editar]Referências
- ↑ Sayan Mukherjee. Lecture 6.5.- Poisson processes. In: PROBABILITY AND STATISTICS IN ENGINEERING.http://www.isds.duke.edu/courses/Fall06/sta113/poisson.pdf
- ↑ V, Guerriero. (2012). "Power Law Distribution: Method of Multi-scale Inferential Statistics". J. Mod. Math. Fr.

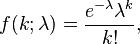
![P[N(t)=K]=\frac{e^{-\lambda t} (\lambda t)^k}{k!},\,\!](http://upload.wikimedia.org/math/e/7/3/e7381820470df4313c45588358ee6ffd.png)

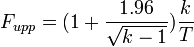
Nenhum comentário:
Postar um comentário