
Na teoria da probabilidade e na estatística, a distribuição de Poisson é uma distribuição de probabilidade discreta que expressa a probabilidade de uma série de eventos ocorrer num certo
período de tempo se estes eventos ocorrem independentemente de quando ocorreu o último evento.
período de tempo se estes eventos ocorrem independentemente de quando ocorreu o último evento.
A distribuição foi descoberta por Siméon-Denis Poisson(1781–1840) e publicada, conjuntamente
com a sua teoria da probabilidade, em 1838 no seu trabalho Recherches sur la probabilité des
jugements en matières criminelles et matière civile ("Inquérito sobre a probabilidade em julgamentos
sobre matérias criminais e civis"). O trabalho focava-se em certas variáveis aleatórias N que contavam,
entre outras coisas, o número de ocorrências discretas (por vezes chamadas de "chegadas")
que tinham lugar durante um intervalo de tempo de determinado comprimento. A probabilidade
de que existam exactamente k ocorrências (k sendo um inteiro não negativo, k = 0, 1, 2, ...) é
com a sua teoria da probabilidade, em 1838 no seu trabalho Recherches sur la probabilité des
jugements en matières criminelles et matière civile ("Inquérito sobre a probabilidade em julgamentos
sobre matérias criminais e civis"). O trabalho focava-se em certas variáveis aleatórias N que contavam,
entre outras coisas, o número de ocorrências discretas (por vezes chamadas de "chegadas")
que tinham lugar durante um intervalo de tempo de determinado comprimento. A probabilidade
de que existam exactamente k ocorrências (k sendo um inteiro não negativo, k = 0, 1, 2, ...) é
onde
- e é base do logaritmo natural (e = 2.71828...),
- k! é o fatorial de k,
- λ é um número real, igual ao número esperado de ocorrências que ocorrem num dado
- intervalo de tempo. Por exemplo, se o evento ocorre a uma média de 4 minutos, e estamos
- interessados no número de eventos que ocorrem num intervalo de 10 minutos, usariámos
- como modelo a distribuição de Poisson com λ = 10/4 = 2.5.
Como função de k, esta é a função de probabilidade. A distribuição de Poisson pode ser derivada
como um caso limite da distribuição binomial.
como um caso limite da distribuição binomial.
Processo de Poisson
A distribuição de Poisson aparece em vários problemas físicos, com a seguinte formulação:
considerando uma data inicial (t = 0), seja N(t) o número de eventos que ocorrem até uma
certa data t. Por exemplo, N(t) pode ser um modelo para o número de impactos de asteróides
maiores que um certo tamanho desde uma certa data de referência.
considerando uma data inicial (t = 0), seja N(t) o número de eventos que ocorrem até uma
certa data t. Por exemplo, N(t) pode ser um modelo para o número de impactos de asteróides
maiores que um certo tamanho desde uma certa data de referência.
Uma aproximação que pode ser considerada é que a probabilidade de acontecer um evento
em qualquer intervalo não depende (no sentido de independência estatística) da probabilidade
de acontecer em qualquer outro intervalo disjunto.
em qualquer intervalo não depende (no sentido de independência estatística) da probabilidade
de acontecer em qualquer outro intervalo disjunto.
Neste caso, a solução para o problema é o processo estocástico chamado de
Processo de Poisson, para o qual vale:
Processo de Poisson, para o qual vale:
em que λ é uma constante (de unidade inversa da unidade do tempo).
Ou seja, o número de eventos até uma época qualquer t é uma distribuição de
Poisson com parâmetro λ t.
Poisson com parâmetro λ t.
[editar]Propriedades
[editar]Média
O valor esperado de uma distribuição de Poisson é igual a λ. Esta propriedade
pode ser derivada facilmente[1]:
pode ser derivada facilmente[1]:
| Em linguagem matemática | Em Português |
|---|---|
![E \left [ X \right ] = \sum_{k=0}^{\infty} k\mathbb{P} \left [ X=k \right ]](http://upload.wikimedia.org/math/c/2/7/c27ac0030882c01f4e3ba068db722b84.png) | Por definição, a esperança de uma variável aleatória X é igual à soma de cada uma das suas possíveis ocorrências ponderadas pela probabilidade de que estas ocorrências aconteçam. |
![E \left [ X \right ] = \sum_{k=0}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!},\,\! \right ]](http://upload.wikimedia.org/math/a/e/b/aebe703a746ffbe5d9b0aa1375ab2ef8.png) | No caso de variáveis com distribuição, a probabilidade de que determinado evento ocorre é calculado por :  . .Portanto, este valor foi substituído na fórmula. |
![E \left [ X \right ] = \begin{matrix} \underbrace{ 0 \left [ \frac{e^{-\lambda} \lambda^0}{0!},\,\! \right ] } \\ k=0 \end{matrix} + \begin{matrix} \underbrace{ 1 \left [ \frac{e^{-\lambda} \lambda^1}{1!},\,\! \right ] } \\ k=1 \end{matrix} + \begin{matrix} \underbrace{ 2 \left [ \frac{e^{-\lambda} \lambda^2}{2!},\,\! \right ] } \\ k=2 \end{matrix}+...](http://upload.wikimedia.org/math/a/d/b/adb0a0229ccc29b8058a3c940151ccf9.png) | Esta expressão equivale à expressão da linha imediatamente superior; apenas se substituiu a expressão de somatório pela soma infinita para melhor compreensão. Note que como o primeiro termo é sempre igual a zero, podemos reescrever ![E \left [ X \right ] = \sum_{k=0}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ] = \sum_{k=1}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ]](http://upload.wikimedia.org/math/6/5/2/6526245ac47e35aab08be5c931a206b9.png) |
Como ![\sum_{k=1}^{\infty} k \left [ \frac{e^{-\lambda} \lambda^k}{k!} \right ]=\sum_{k=1}^{\infty} \lambda \left [ \frac{e^{-\lambda} \lambda^{k-1}}{(k-1)!} \right ]](http://upload.wikimedia.org/math/7/a/8/7a8c7133c2ec82362fa9aa9c077e1c1e.png) | Fazemos uma substituição para facilitar o cálculo. |
![E \left [ X \right ] =\lambda \sum_{k=1}^{\infty} \left [ \frac{e^{-\lambda}\lambda^{k-1}}{(k-1)!} \right ]](http://upload.wikimedia.org/math/6/2/b/62b46c1939d2c2ea1dedac233921c625.png) | Tomamos a substituição acima e tiramos a constante  para fora do somatório (pois o primeiro termo da expressão imediatamente superior é igual à para fora do somatório (pois o primeiro termo da expressão imediatamente superior é igual à  . . |
![E \left [ X \right ] = \lambda e^{-\lambda} \sum_{k=0}^{\infty} \left [ \frac{\lambda^{k}}{(k)!} \right ]](http://upload.wikimedia.org/math/b/e/6/be60a9e58ce6cc3ae36bbdf2e866896d.png) | Nova transformação para facilitar os cálculos... |
![E \left [ X \right ] = \lambda e^{-\lambda}](http://upload.wikimedia.org/math/2/6/d/26d1a16606b089bdf4cda7ebd2193d9b.png) ![\left [ \frac{\lambda^{0}}{(0)!}+ \frac{\lambda^{1}}{(1)!}+ \frac{\lambda^{2}}{(2)!}+\frac{\lambda^{3}}{(3)!}+... \right ]](http://upload.wikimedia.org/math/a/f/7/af767888596668554224b683dd2de9ba.png) | Abrindo o somatório, verifica-se que a série converge para  |
![E \left [X \right] = \lambda e^{-\lambda}e^{\lambda}](http://upload.wikimedia.org/math/8/b/7/8b75ff3b01bac2b16b47bf95e664c8fa.png) | Obtemos  |
![E \left [ X \right ] = \lambda](http://upload.wikimedia.org/math/e/1/7/e1757adeca54855d6ff40534c4d6d6aa.png) | Como queríamos demonstrar |
[editar]Variância
A variância de uma distribuição de Poisson é igual a λ.
[editar]Soma de variáveis
A soma de duas variáveis de Poisson independentes é ainda uma variável de Poisson com parâmetro igual à soma dos respectivos parâmetros. Ou seja, se  segue uma distribuição de Poisson com parâmetro
segue uma distribuição de Poisson com parâmetro  e as variáveis aleatórias
e as variáveis aleatórias  são estatisticamente independentes, então
são estatisticamente independentes, então
 segue uma distribuição de Poisson com parâmetro
segue uma distribuição de Poisson com parâmetro  e as variáveis aleatórias
e as variáveis aleatórias  são estatisticamente independentes, então
são estatisticamente independentes, então-
 também segue uma distribuição de Poisson cujo parâmetro é igual à soma dos
também segue uma distribuição de Poisson cujo parâmetro é igual à soma dos  .
.
Por exemplo, 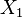 é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e  é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média 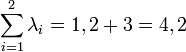 .
.
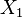 é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "A" (distribuição de Poisson com média 1,2, digamos) e  é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média
é uma variável aleatória que representa o número de óbitos por mil nascimentos na cidade "B" (variável de Poisson com média 3). Ao todo, o número de óbitos por mil nascimentos nas cidades "A" e "B" têm distribuição de Poisson com média 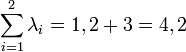 .
.[editar]Intervalo de confiança
Um método rápido e fácil para calcular um intervalo de confiança de aproximada de λ, é proposto na Guerriero (2012)[2]. Dado um conjunto de eventos k (pelo menos 15 - 20) ao longo de um período de tempo T, os limites do intervalo confiança para a frequência são dadas por:
em seguida, os limites do parâmetro  são dadas por:
são dadas por:  .
.
 são dadas por:
são dadas por:  .
.[editar]Exemplos
A distribuição de Poisson representa um modelo probabilístico adequado para o estudo
de um grande número de fenômenos observáveis.
Eis alguns exemplos:
de um grande número de fenômenos observáveis.
Eis alguns exemplos:
- Chamadas telefônicas por unidade de tempo;
- Defeitos por unidade de área;
- Acidentes por unidade de tempo;
- Chegada de clientes a um supermercado por unidade de tempo;
- Número de glóbulos sangüíneos visíveis ao microscópio por unidade de área;
- Número de partículas emitidas por uma fonte de material radioativo por unidade de
tempo.
[editar]Referências
- ↑ Sayan Mukherjee. Lecture 6.5.- Poisson processes. In: PROBABILITY AND
- STATISTICS IN ENGINEERING.http://www.isds.duke.edu/courses/Fall06/sta113/poisson.pdf
- ↑ V, Guerriero. (2012). "Power Law Distribution: Method of Multi-scale Inferential Statistics". J. Mod. Math. Fr.
fonte wikipédia
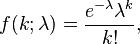
![P[N(t)=K]=\frac{e^{-\lambda t} (\lambda t)^k}{k!},\,\!](http://upload.wikimedia.org/math/e/7/3/e7381820470df4313c45588358ee6ffd.png)

Nenhum comentário:
Postar um comentário